


作者:鄂维南院士
本文是鄂维南院士对数据科学这个全新学科的定义。摘自高等教育出版社《数据科学导引》教材的绪论部分。
什么是数据科学?它和已有的信息科学、统计学、机器学习等学科有什么不同?作为一门新兴的学科,数据科学依赖两个因素:一是数据的广泛性和多样性;二是数据研究的共性。现代社会的各行各业都充满了数据,这些数据的类型多种多样,不仅包括传统的结构化数据,也包括网页、文本、图像、视频、语音等非结构化数据。数据分析本质上都是在解反问题,而且通常是随机模型的反问题,因此对它们的研究有很多共性。例如,自然语言处理和生物大分子模型都用到隐马尔科夫过程和动态规划方法,其最根本的原因是它们处理的都是一维随机信号;再如,图像处理和统计学习中都用到的正则化方法,也是处理反问题的数学模型中最常用的一种。
数据科学主要包括两个方面:用数据的方法研究科学和用科学的方法研究数据。前者包括生物信息学、天体信息学、数字地球等领域;后者包括统计学、机器学习、数据挖掘、数据库等领域。这些学科都是数据科学的重要组成部分,只有把它们有机地整合在一起,才能形成整个数据科学的全貌。
如何用数据的方法研究科学
用数据的方法研究科学,最典型的例子是开普勒关于行星运动的三大定律。开普勒的三大定律是根据他的前任,一位叫第谷的天文学家留给他的观察数据总结出来的。表1列出的观测数据是行星绕太阳一周所需要的时间(以年为单位)和行星离太阳的平均距离(以地球与太阳的平均距离为单位)。从这组数据可以看出,行星绕太阳运行的周期的平方和行星离太阳的平均距离的立方成正比,这就是开普勒第三定律。

图1 用数据的方法研究科学的典型例子:开普勒三大定律
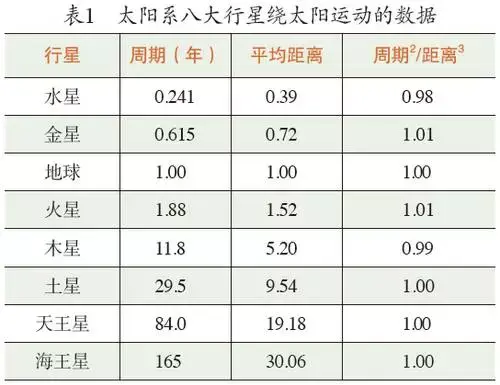
开普勒虽然总结出他的三大定律,但他并不理解其内涵。牛顿则不然,他用牛顿第二定律和万有引力定律把行星运动归结成一个纯粹的数学问题,即一个常微分方程组。如果忽略行星之间的相互作用,那么各行星和太阳之间就构成了一个两体问题,我们很容易求出相应的解,并由此推导出开普勒的三大定律。
牛顿运用的是寻求基本原理的方法,它远比开普勒的方法深刻。牛顿不仅知其然,而且知其所以然。所以牛顿开创的寻求基本原理的方法成为科学研究的首选模式,这种方法的发展在20世纪初期达到了顶峰,在它的指导下,物理学家们提出了量子力学。原则上讲,我们在日常生活中看到的自然现象都可以从量子力学出发得到解释。量子力学提供了研究化学、材料科学、工程科学、生命科学等几乎所有自然和工程学科的基本原理,这应该说是很成功的,但事情远非这么简单。狄拉克指出,如果以量子力学的基本原理为出发点去解决这些问题,那么其中的数学问题就太困难了。因此必须妥协,对基本原理作近似。
尽管牛顿模式很深刻,但对复杂的问题,开普勒模式往往更有效。例如,表2中形象地描述了一组人类基因组的单核苷酸多态性(Single Nucleotide Polymorphism, SNP)数据。研究人员在全世界挑选出1064个志愿者,并把他们的SNP数据数字化,即把每个位置上可能出现的10种碱基对用数字表示,对这组数据做主成分分析(PCA)——一种简单的数据分析方法,其原理是对数据的协方差矩阵做特征值分解,可以得到图2所示的结果。其中横轴和纵轴分别代表第一和第二奇异值所对应的特征向量,这些向量一共有1064个分量,对应1064个志愿者。值得注意的是,这组点的颜色所代表的意义。由此可见,通过最常见的统计分析方法——主成分分析,可以从这组数据中展示出人类进化的过程。
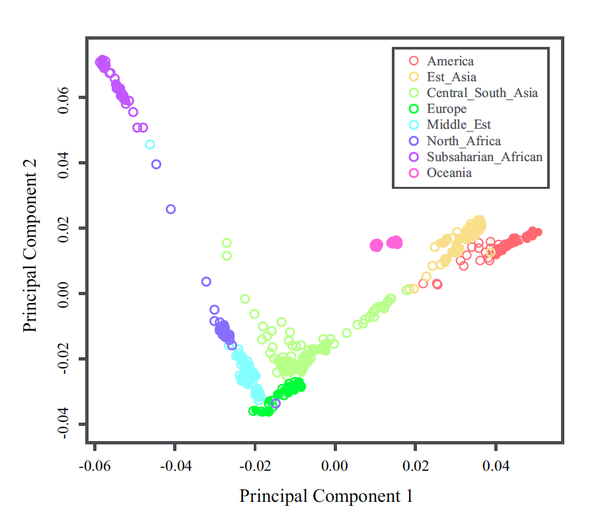
图2 对SNP数据做主成分分析的结果[1]
如果采用从基本原理出发的牛顿模式,上述问题基本是无法解决的,而基于数据的开普勒模式则行之有效。开普勒模式最成功的例子是生物信息学和人类基因组工程,正因为它们的成功,材料基因组工程等类似的项目也被提上了议程。同样,天体信息学、计算社会学等也成为热门学科,这些都是用数据的方法研究科学问题的例子。而图像处理是另一个典型的例子。图像处理是否成功是由人的视觉系统决定的,要从根本上解决图像处理的问题,就需要从理解人的视觉系统着手,理解不同质量的图像对人的视觉系统会产生什么样的影响。当然,这样的理解很深刻,而且也许是我们最终需要的,但目前看来,它过于困难也过于复杂,解决很多实际问题时并不会真正使用它,而是使用一些更为简单的数学模型。
用数据的方法研究科学问题,并不意味着就不需要模型,只是模型的出发点不一样,不是从基本原理的角度去寻找模型。以图像处理为例,基于基本原理的模型需要描述人的视觉系统以及它与图像之间的关系,而通常的方法可以是基于更为简单的数学模型,如函数逼近的模型。
如何用科学的方法研究数据
用科学的方法研究数据主要包括数据采集、数据存储和数据分析。本文将主要讨论数据分析。
数据分析的中心问题
比较常见的数据有以下几种类型。
1.表格:最为经典的数据类型。在表格数据中,通常行代表样本,列代表特征;
2.点集(point cloud):很多数据都可以看成是某空间中的点的集合;
3.时间序列:文本、通话和DNA序列等都可以看成是时间序列。它们也是一个变量(通常是时间)的函数;
4.图像:可以看成是两个变量的函数;
5.视频:时间和空间坐标的函数;
6.网页和报纸:虽然网页或报纸上的每篇文章都可以看成是时间序列,但整个网页或报纸又具有空间结构;
7.网络数据:网络本质上是图,由节点和联系节点的边构成。
除了上述基本数据类型外,还可以考虑更高层次的数据,如图像集、时间序列集、表格序列等。
数据分析的基本假设是观察到的数据都是由某个模型产生的,而数据分析的基本问题就是找出这个模型。由于数据采集过程中不可避免会引入噪声,因此这些模型都是随机模型。例如,点集对应的数据模型是概率分布,时间序列对应的数据模型是随机过程,图像对应的数据模型是随机场,网络对应的数据模型是图模型和贝叶斯模型。
通常我们对整个模型并不感兴趣,而只是希望找到模型的一部分内容。例如我们利用相关性来判断两组数据是否相关,利用排序来对数据的重要性进行排名,利用分类和聚类将数据进行分组等。
很多情况下,我们还需要对随机模型作近似。最常见的方法是将随机模型近似为确定型模型,所有的回归模型和基于变分原理的图像处理模型都采用了这种近似;另一类方法是对其分布作近似,例如假设概率分布是正态分布或假设时间序列是马尔科夫链等。
数据的数学结构
要对数据作分析,就必须先在数据集上引入数学结构。基本的数学结构包括度量结构、网络结构和代数结构。
1. 度量结构。在数据集上引进度量(距离),使之成为一个度量空间。文本处理中的余弦距离函数就是一个典型的例子。
2. 网络结构。有些数据本身就具有网络结构,如社交网络;有些数据本身没有网络结构,但可以附加上一个网络结构,例如度量空间的点集,我们可以根据点与点之间的距离来决定是否把两个点连接起来,这样就得到一个网络结构。网页排名(PageRank)算法是利用网络结构的一个典型例子。
3. 代数结构。把数据看成向量、矩阵或更高阶的张量。有些数据集具有隐含的对称性,也可以用代数的方法表达出来。
在上述数学结构的基础上,可以讨论更进一步的问题,例如拓扑结构和函数结构。
1. 拓扑结构。从不同的尺度看数据集,得到的拓扑结构可能是不一样的。最著名的例子是3×3的自然图像数据集里面隐含着一个二维的克莱因瓶(Klein bottle)。
2. 函数结构。对点集而言,寻找其中的函数结构是统计学的基本问题。这里的函数结构包括线性函数(用于线性回归)、分片常数(用于聚类或分类)、分片多项式(如样条函数)、其他函数(如小波展开)等。
数据分析的主要困难
我们研究的数据通常有几个特点:
1、数据量大。数据量大给计算带来挑战,需要一些随机方法或分布式计算来解决问题;
2、数据维数高。例如,前面提到的SNP数据是64万维的;
3、数据类型复杂。网页、报纸、图像、视频等多种类型的数据给数据融合带来困难;
4、噪音大。数据在生成、采集、传输和处理等流程中,均可能引入噪音,这些噪音的存在给数据清洗和分析带来挑战,需要有一定修正功能的模型(如图像中的正则化和机器学习中的去噪自编码器)来进行降噪处理。
其中,最核心的困难是数据维数高。它会导致维数灾难(curse of dimensionality),即模型的复杂度和计算量随着维数的增加而指数增长。那么,如何克服数据维数高带来的困难?通常有两类方法。一类是将数学模型限制在一个极小的特殊类里,如线性模型;另一类是利用数据可能有的特殊结构,如稀疏性、低维、低秩和光滑性等。这些特性可以通过对模型作适当的正则化实现,也可以通过降维方法实现。
总之,数据分析本质上是一个反问题。处理反问题的许多方法(如正则化)在数据分析中扮演了重要角色,这正是统计学与统计力学的不同之处。统计力学处理的是正问题,统计学处理的是反问题。
算法的重要性
与模型相辅相成的是算法以及这些算法在计算机上的实现。在数据量很大的情况下,算法的重要性尤为突出。从算法的角度来看,处理大数据主要有两条思路:
1. 降低算法的复杂度,即计算量。通常要求算法的计算量是线性标度的,即计算量与数据量成线性关系。但很多关键的算法,尤其是优化方法,还达不到这个要求。对于特别大的数据集,如万维网上的数据或社交网络数据,我们希望能有次线性标度的算法,也就是说计算量远小于数据量。这就要求我们采用抽样的方法。其中最典型的例子是随机梯度下降法(Stochastic Gradient Descent, SGD)。
2. 分布式计算。其基本思想是把一个大问题分解成很多小问题,然后分而治之。著名的MapReduce框架就是一个典型的例子。
现阶段,算法的研究分散在两个基本不相往来的领域——计算数学和计算机科学。计算数学研究的算法主要针对像函数这样的连续结构,其主要应用对象是微分方程等;计算机科学主要处理离散结构,如网络。而现实数据的特点介于两者之间,即数据本身是离散的,而数据背后有一个连续的模型。因此,要发展针对数据的算法,就必须把计算数学和计算机科学研究的算法有效地结合起来。
作者:鄂维南

×××院士、美国数学学会、美国工业与应用数学学会会士。普林斯顿大学数学系和应用数学研究所教授、北京大学国际数学研究中心和数学学院教授、北京大数据研究院院长。
参考文献:
[1] Jun Z. Li, et al.,Worldwide Human Relationships Inferred from Genome-Wide Patterns of Variation, Science 319, 1100 (2008).
